第1部 相対論における空間の問題
4 いわゆるローレンツ収縮がありうるとしたら
この条件で、どのような時間が可能になるのか。100の時間軸が彼自身の中で同時進行する、という考え方を検討するべきかどうかわからない。多世界解釈も含めて、私は全く価値を認めたくはないと思うのだが、納得できる語り方がありえるなら、読んでみたいと思う(ただし後で検討し、それが全くのナンセンスであることは述べておくつもりだ)。
たいていは、時間のずれを相手方に押し付ける、つまりラジコンカーやドローンがそれぞれの時間軸を動く、という形に、何となく収まるのではないだろうか。これは理論的にそう考えるというのではなく、あまり追求せずぼんやりとしたままに意識の片隅に追いやるという感覚だ。時間という観念のあいまいさが、あいまいなままにしておくことを許す。
今、とりあえず時間について考えてみたのは、たとえ矛盾があっても時間が主題である限り人はその矛盾にあまりこだわらない、ということを示すためだった。相対論は時間と空間の革命的理論であると多くの人は認識しているので、最大限に抽象的なところから考えてしまう悪弊にどうしても囚われてしまうが、もう少し現実的な考え方から入るべきなのだろう。
たとえば高速移動中のものは進行方向に縮むということは、相対論の帰結としては有名な部類だ。では精密で古典的な機械、懐中時計を高速移動させたらどうなるか。まあ、デジタルデバイスでもよいのだが、直感的にわかりやすいもので考えることにする。
懐中時計を用意し、文字盤を真正面から見据える形にして、左右どちらかの方向に動かすと、これは左右につぶれた、いびつな円形になる。
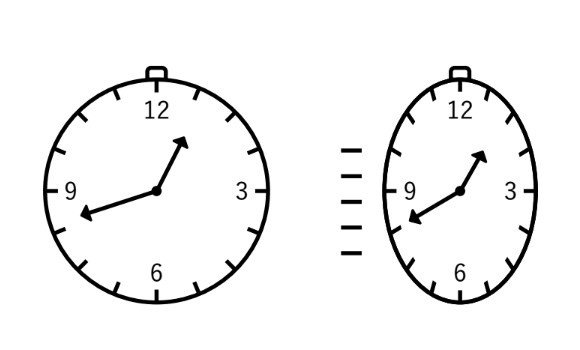
では、右に示した側は、中の歯車もいびつな円形になるはずだ。それでどうして時が刻めるのだろうか。いびつな円形への変化が真に物理的な効果を伴うものであれば、または物理的な原因によるものならば、いびつな円形の歯車を正確にかみ合わせて、なおかつ縦長の形状を維持したままで回すことなどできない。
相対論には少なくとも、そういう奇怪な現象を支持する式は存在しないはずだ。ここを間違ってはならない。あるのは、進行方向に縮むという計算式だけである。














