【前回の記事を読む】納得できる二階微分方程式の解法をここに!筆者が解き明かす数式の裏側
第2章 文字積分法で拓く連立微分方程式の解法
第1章では二階微分方程式を解いて三角関数の冪級数を導出しました。
第2章は円の連立微分方程式を解いて三角関数を導くまでの解説です。
解法には
・数値積分による解法
・文字積分による解法
・論理図解による解法
の3つの解法があり、3節に分けて解説します。
第1節 数値積分による解法
【案内】数値積分による解法にはExcelの表計算による解法と、Visual BASICによる数値積分法の2つがあります。
その1 表計算
・第一段階 円を表わす方程式
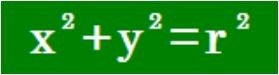
・第二段階 円を表わす連立微分方程式

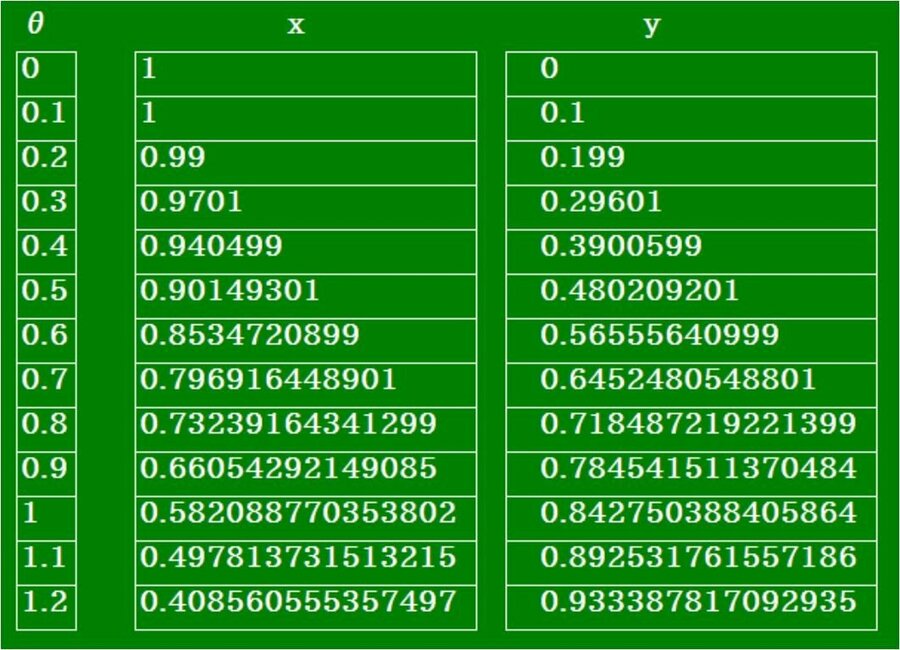
・第三段階 表計算による数値積分
【案内】表計算をまねたVisual BASIC で計算します。
ε=dθはこの後で示されます。

・オイラー法で円を作図するときのプロシージャは付録 コンピュータープログラムの紹介に記述します。
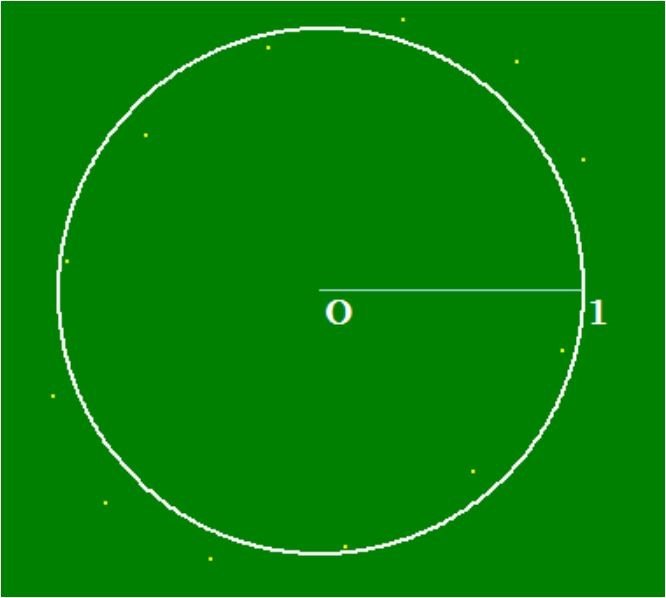
・εを大きめにとると、崩れた円を描きますが、微小にとると完全な円に近づきます。
ε=0.5では13個の点ですが、ε=0.001では円のグラフになります。