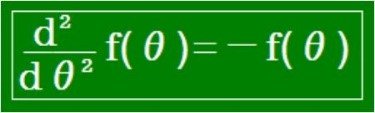第1章 文字積分法で拓く二階微分方程式の解法
三角関数が理解しにくい理由は、弧度法の定義が不十分だからです。しかし、発明者と時代についての詳細な記録がないのです。そのため筆者独自の考察で推理を進めました。
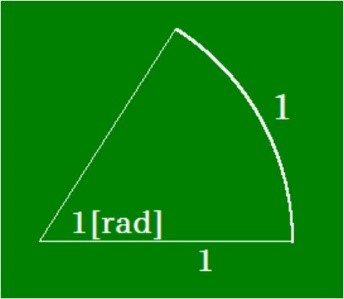
弧度法は次の図で定義されています。単位円の半径の1と弧の長さの1とそして角度の1[rad]です。
弧度法を取り入れた座標系が「極座標」です。直角座標系との変換公式も表示します。
変換公式ではcosθとsinθが使われていますが、あくまでもcosθとsinθでなければならないのです。関数cosθとsinθは次の二階微分方程式の解です。そして、これに間違いはないのです。
数学者はこの解説ができないことに困っています。前記のような解説が高等学校の数学の教科書に掲載されることはありませんでした。証明できないので掲載できなかったからと思います。
弧度法の定義で弧の1をθにし、1[rad]をθ[rad]にするところまでは進めても、座標P(cosθ,sinθ)を付け加えることができないのです。この証明は拙著『理系教科書補助教材』(2011年 PHPパブリッシング刊行)に記載しました。
この解はすでに知られています。 f(θ)=Acosθ+Bsinθです。従ってこれ以上学ぶ必要はないのです。しかし、「同じ解法で三階微分方程式を解いてください」と依頼しても、断られると思います。三階微分方程式は2000年に筆者が解きましたが、当然cosθもsinθも現れません。