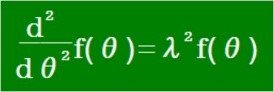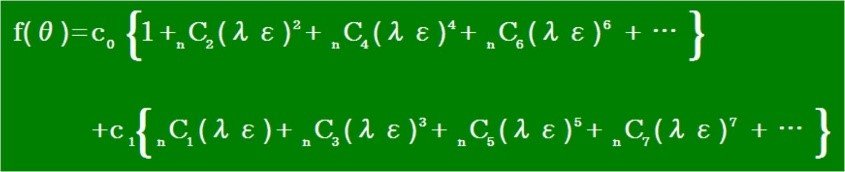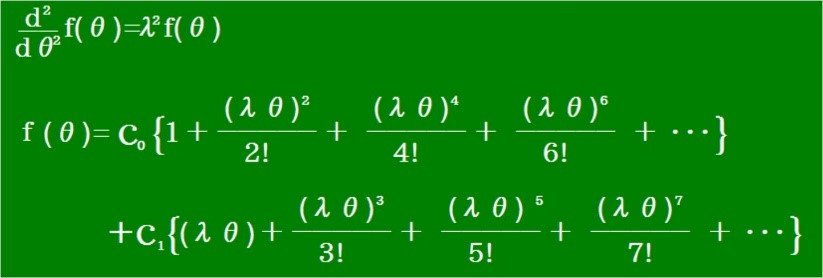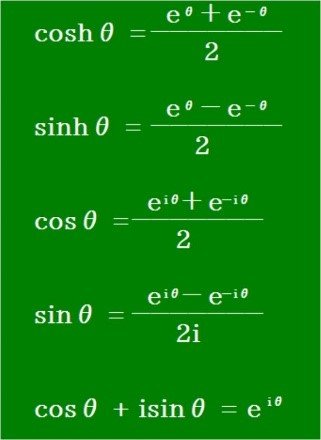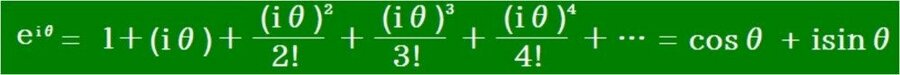学校で学ぶ数々の公式の「モヤモヤ感」筆者がそれ解き明かします！

第1節　二階微分方程式の新情報

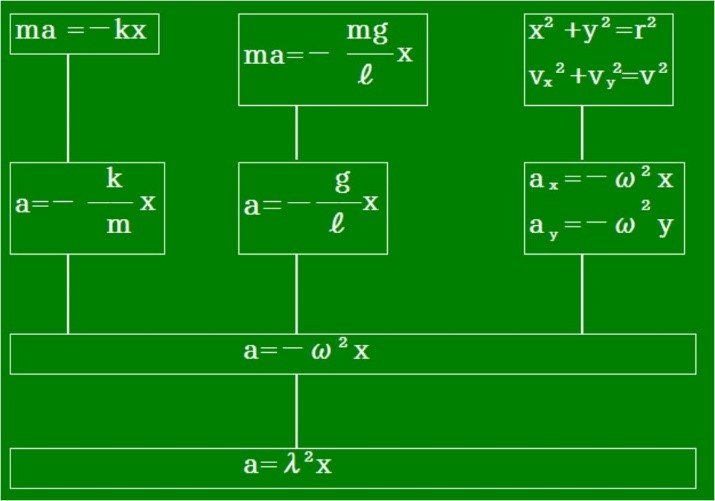
【文字積分法】を使った二階微分方程式の解法を示します。単振動を表わすいろいろな二階微分方程式です。

上記の3つの微分方程式は、次の式で代表されます。ここでλ＝iωです。

つぎに、この微分方程式を文字積分法で解きます。

第1段階　文字積分法

【解法のヒント】初期条件は　f(0)=c₀  f⁽¹⁾(0)=c₁λ となります。この初期条件に気付くまでに、相当な時間を費やしましたが、ここからは表計算と同じ計算法です。

【数値積分法】という名称はすでにあります。【文字積分法】は筆者の命名です。

第2段階　θ=nεにおけるf(θ)の冪関数の予想

c₀とc₁の2つの項に分離すると規則性が見えてきます。

第3段階　変換公式の準備

第2段階から第4段階に式を変形するときには次の変換公式を使います。重要な式です。

【注目】「第2章 第2節　文字積分による解法」でも使います。

第4段階 【結論】

二階微分方程式とその解です。

関数の初期条件はf(0) = c₀ で  f⁽¹⁾(0)=c₁λ となります。

第5段階

【発展】前段階の解は次に述べる関数群となって出現します。

数学では個々の関数とされましたが、「共通の基礎」となる微分方程式が見落とされてきましたことになります。

ここで、関数cosθとsinθを定義しておくと論理が整理されます。

二階微分方程式の解は、次のように　e^θ,e^－θ,^eiθ,e^－iθ　つまり e^λθの形式でも表わされています。

【発見】オイラーの公式の証明は無意味

関数群の中で、c₀ =1、c₁=1、λ=iとしたときは　2つの表示法があります。表現方法の違いなので、左辺と右辺とは当然一致しています。証明以前の事実です。次の式のモヤモヤ感は消えました。

数学では関数e^θのθにiθを代入してオイラーの法則の証明としています。無意味な証明でモヤモヤが残ります。この第1節で「文字積分法」を使い、明解な証明ができたことになります。