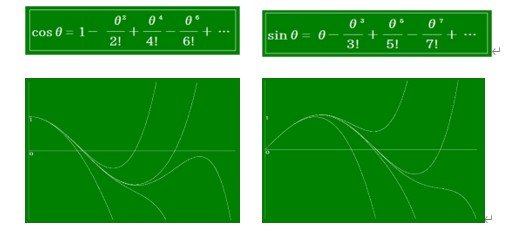
第2節 冪三角関数で円を描く
前節の関数群のうち、関数cosθとsinθについてグラフを描きます。2つの関数はθの関数であることが明らかになりましたので、点P(cosθ,sinθ)が円を描くことを証明します。
二階微分方程式と連立微分方程式とに共通しているcosθとsinθを使い、コンピューターで作図しました。左が冪余弦関数で右が冪正弦関数です。
数学では、この解eλθを仮定した微分方程式の解法があります。
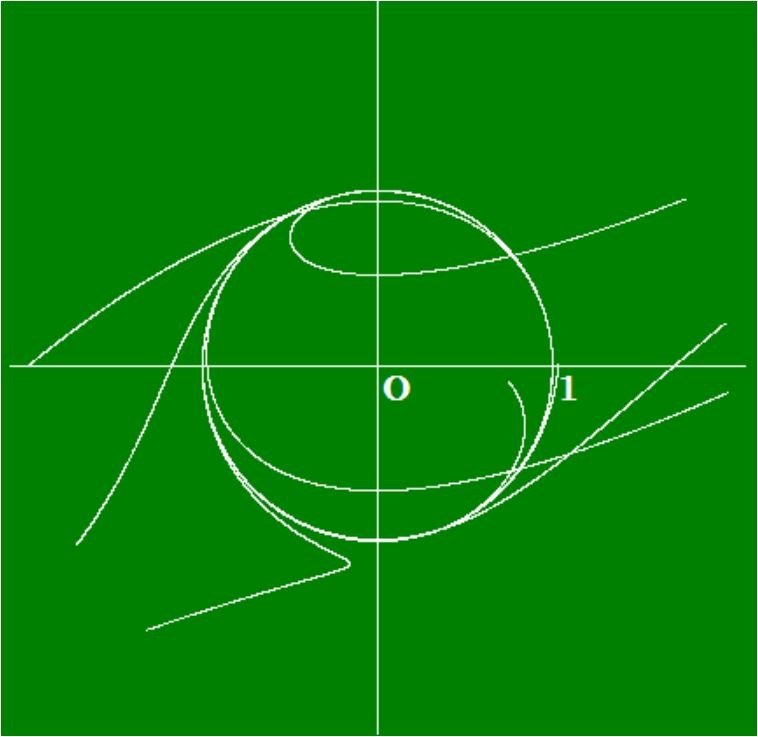
冪級数の中の関数θnでn→∞ にすると、確かに円を描きます。しかし、高次の関数でなくても円にかなり近いグラフを描くことができます。
低次の関数で特徴的な関数を使うと顔の形ができます。拙著『丸で歯が立たない円の秘密』の表紙にしました。目はΘを使いました。