第5章 物理学と三角関数
第2節 単振動と三角関数
【案内】高校の数学や物理学では二階微分方程式の解を既知とします。
・高等学校の物理学で最も難しいと思われる項目は、「単振動」です。
理論は数学にまかせて、物理学では次の公式から始めることになります。弧度法は素通りします。
x= Acosωt + Bsinωtは a=-ω2xの解です。
しかし、逆の証明は難しく、物理学と数学の両方で困っています。
a=-ω2x を解き、x= Acosωt + Bsinωtを求めなさい。
【案内】筆者はこの困難を以下のように文字積分で乗り切りました。
・『第1章第1節 二階微分方程式の新解法』から次の解が求められていました。
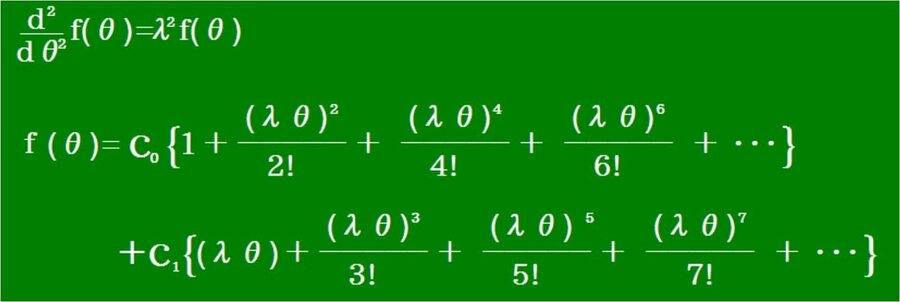
ここで、θを時刻t、f(t)を位置 x、f(2)(t)を加速度aとし、さらにλ=iω と置き換えると、
a =-ω2x x = c0cosωt + ic1sinωt
さらに c0 = A ic1 = B と置き換えると x = Acosωt + Bsinωt となります。単振動の解です。
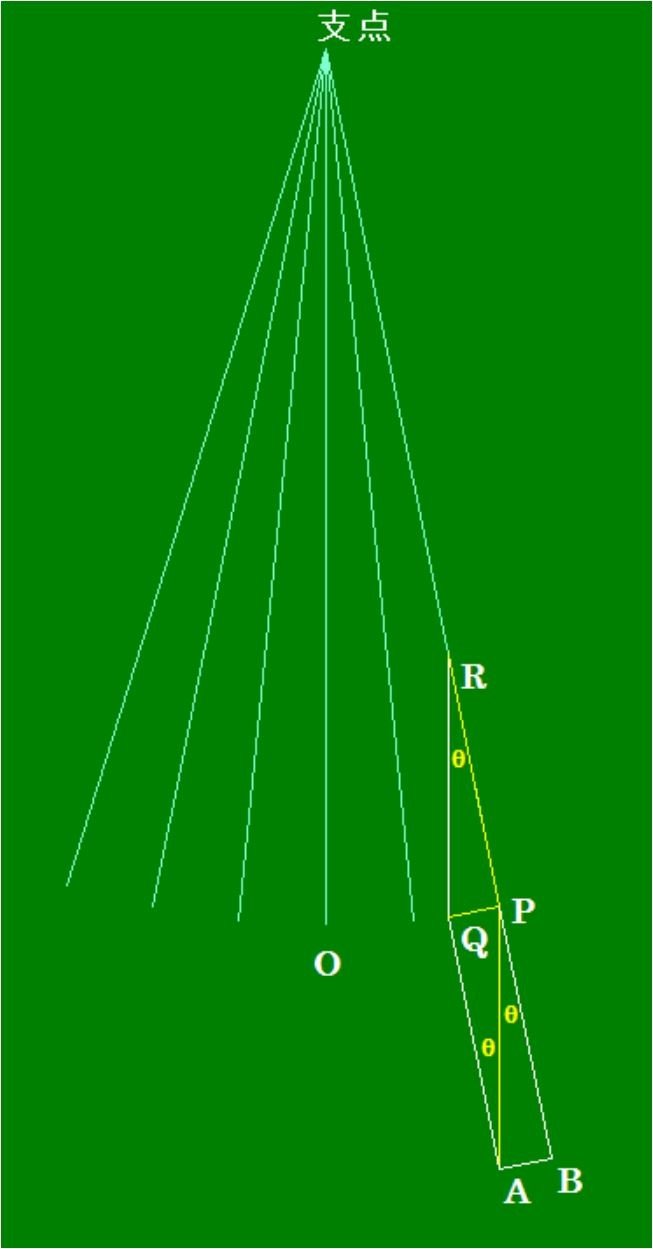
・単振り子の解
ガリレオ・ガリレイの振り子での周期の話は有名です。θが小さい時には単振動です。

・物理学での等速円運動
高等学校の物理学の教科書の特徴は、平面座標系を使った解説がないことです。大学では、物理学は座標を使いますからつまずきます。さらに、物理学は文字としてx,y,r,θ,ω,tの6つを使います。
・円運動における動点の位置を、最初からP(rcosωt,rsinωt)として表わしています。動点ですから捉えどころのない感覚をもってしまうのです。
・θの定義を明確にして、P(rcosθ,rsinθ)から始める解説に変更する必要があります。その後にθ=ωt として考察を進めます。