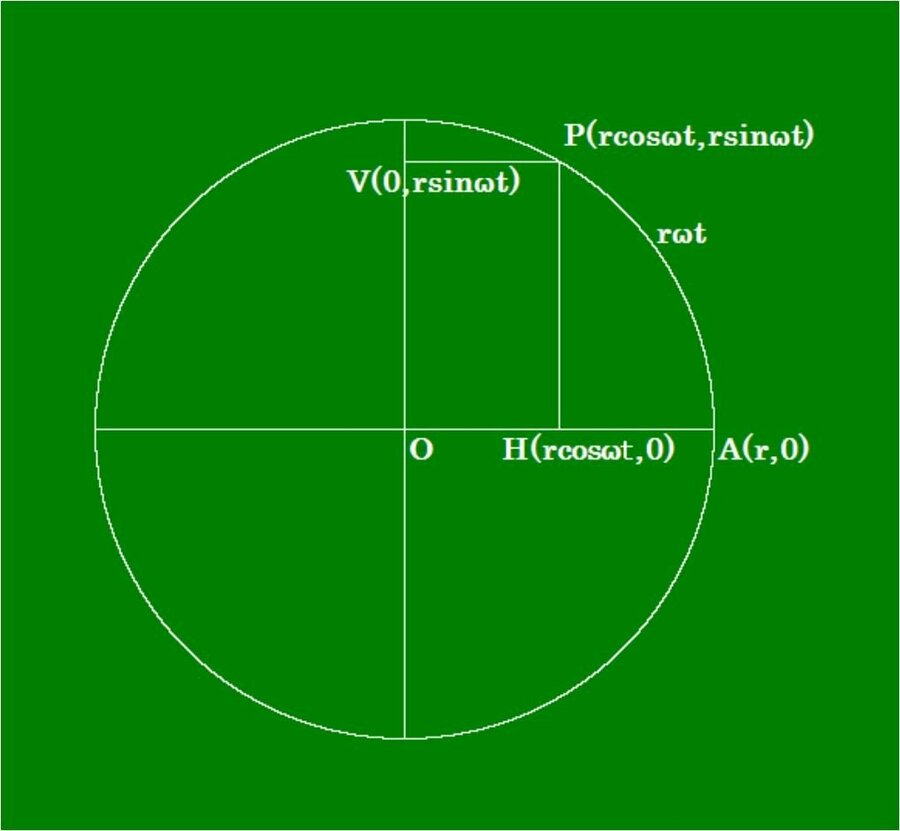
【角振動数】等速円運動における角回転数と単振動における角振動数との関係
動点P(rcosωt,rsinωt)の射影点となるH(rcosωt,0)やV(0,rsinωt)は単振動の点になります。
この時は直線運動になりますから、ωを角回転数とするのも無理があり、角振動数と言います。
・角回転数と角振動数をインターネットで検索してもなかなかみつかりません。無視されています。
・【インターネットでの角速度の解説の誤り】
つぎのように角速度と慣性の法則とをぶつけると矛盾していることが分かります。
円運動について、速度vと半径rと角速度ωに関しては、次のような具体例を考えます。半径1[m]の円周上を角速度1[rad・m/s]で回転している物体の糸が突然切れました。慣性の法則から、物体は速さ1[m/s]の直線運動をして離れていきます。
問 いつの間に[rad]が吹っ飛ぶのでしょう。最初から[rad]は入れてはいけないのです。
・高等学校の物理学の教科書には角速度ばかりで角回転数の記述はほとんどありません。大学受験参考書も同様です。
・高校生が次のように理解していれば問題ありません。
半径がr[m]の円で、中心角θ[rad]に対応する円弧の長さはrθ[m]です。
rθのrに単位[m]はつきますが、θには単位はつきません。
・インターネットの解説や大学入試問題での三角関数の取り扱いの間違い
ωを角速度として、円運動の位置(x,y)を表わすと x=rcosωt y=rsinωt となります。
ωを角速度として単位として[rad/s]を使うと三角関数を使用できなくなります。誤った式です。
・「角速度ωの単位は[rad/s]ですが数量としては角回転数[1/s]と同じになります」として、三角関数の中でωを強引に使っているのが現状でしょう。