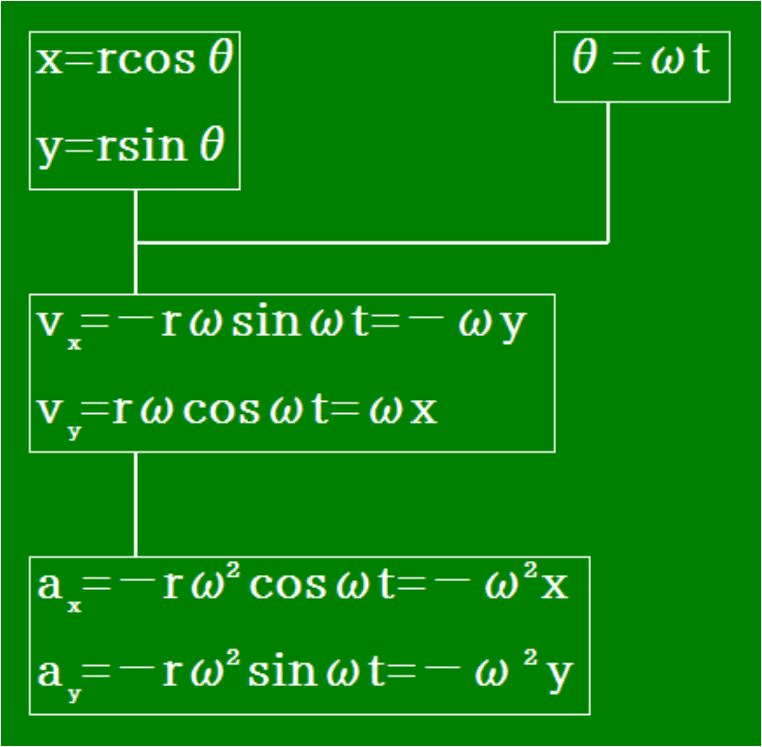第5章 物理学と三角関数
第2節 単振動と三角関数
【角度と角度の大きさの違い】
角度の問題として「弧度法の意味を図に描いて解説してください」はどうでしょう。
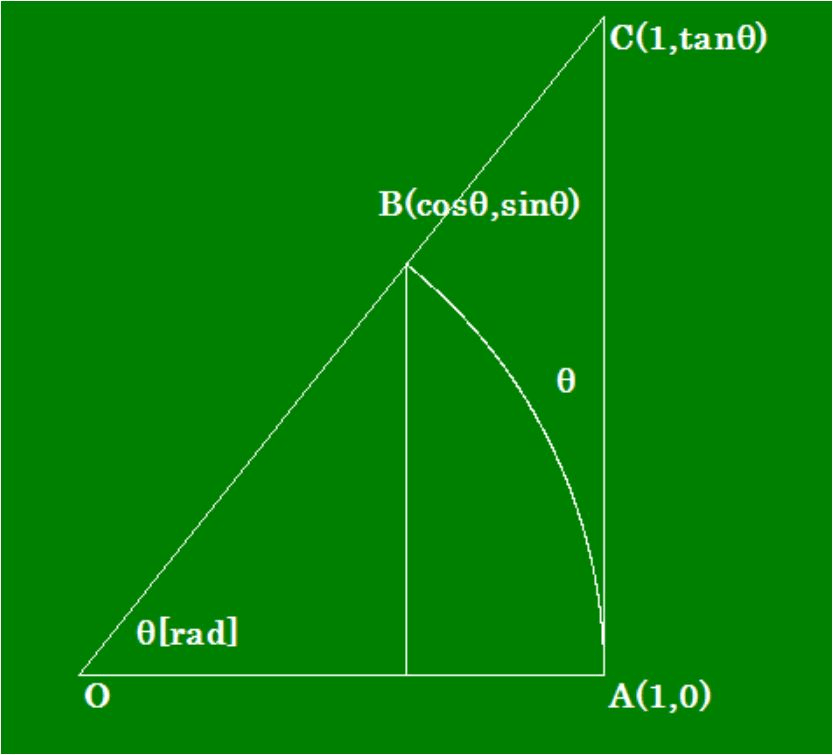
・θの名称はまだない
単位円において、角度Θ=θ[rad]に対応する弧の長さがθで、名称はまだなく、単位はつきません。半径の何倍かを示す数値です。
・辞典やインターネット検索の中から角回転数の用語が見当たりません。歴史的に、ωは角速度と角回転数の両方で使われてきました。2022年9月現在、インターネット検索では「角回転数」は極端に少なく、「角速度」がほとんどです。
・θ→0になるとsinθ→θでθ[rad]となりません。
・角速度と角回転数の大きな違いは、cosθと sinθのθには単位がつかないことです。もし、θ→0 になると sinθ→θ であり、θ[rad]ではありません。θ=ωtとすると、tの単位は[s]で、ωの単位は[1/s]になります。この時は、角回転数なのです。
・円運動の速度と加速度を正確に記述しましょう。等速円運動の速度と加速度では、大学生には次のようなレポート問題が適当でしょう。高等学校では、平面座標での解説はありません。大学では正確に解説する必要があります。
答は速度と加速度の明示になるでしょう。正しく速度と加速度を記述しなければなりません。「第5章第1節等速円運動における速度と加速度」に記述してあります。速度には時計回りと反時計回りの2組の式があります。加速度の式は1組です。
第3節 速度と加速度はベクトルである証明
【案内】第1節で等速円運動における加速度がベクトルであることを証明しました。ここでは三角関数で証明します。
・数学や物理学の本や教科書でのベクトルの扱い方の修正が必要です。物理学の教科書では、最初に速度や加速度をベクトルと決めておいてから、作図から速度と加速度を求めています。論理の向きが逆です。さらに、作図では[rad]も加えていますから、この段階ですでに間違いです。
・三角関数でωを角回転数として取り扱い、cosθとsinθとにθ=ωtを代入します。
・等速円運動における加速度は原点を向き、大きさがrω2となる証明です。