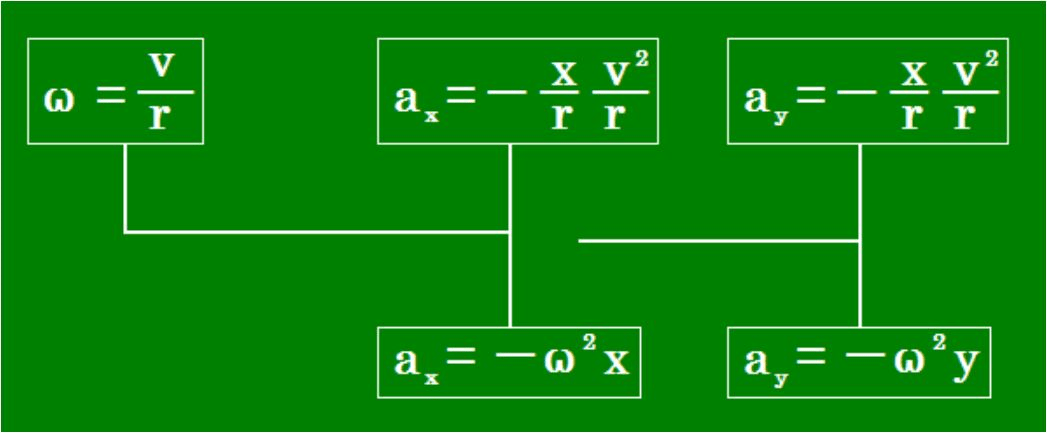
・「第5章 第1節 等速円運動における速度と加速度」から速度と加速度は向きと大きさとを持ち、ベクトルであることが証明できました。第5章第1節の結論の加速度と比較すると、ω=v/rであることが明らかです。
・2022年以前の大学入試問題では数学の内容は、整数分野の出題が多く実数を取り扱う物理学関連の出題は極めて少なくなっています。今まで物理学方面の出題に誤りが多かったのが原因と思います。
・筆者が弧度法を再検討しようと考えたのは次の書籍を読んだからです。
長谷川節(はせがわみさお) 著( 1994年 株式会社近代文藝社 刊行)
あとがきの最後の文章には感銘を受けます。
第4節 等速円運動における変数の関連図解
・(道のり)= rθの左辺と右辺の単位は同じく[m]で、(道のり)と半径rの単位は共に[m]ですからθには単位はなく数値なのです。つまりθに[rad]はつきません。
・円運動だけ特別に(道のり)の単位を[rad・m]にすると考えることはありえないでしょう。

第5節 回転数と角回転数
拙著『オイラーの公式は一行で証明できる』の中に【短い小説】ある国でロケットが爆発という一文を掲載しました。テレビのニュースでロケットが発射後に爆発したことを伝えたからでした。
【論点】筆者は高校生の時に、交流電圧は V=V0sin(2πft)となることを知りました。2πに単位はつかずf=50あるいは60で単位は[Hz]あるいは[1/s]で、tは時刻で単位は[s]です。従って、2πft全体では単位はつきません。さらに、V=V0sinωt の表現もありましたが、流れから2πf=ωとなり、単位は[1/s]です。
fの名称が周波数ですが、ωの名称は気に留めていませんでしたが「角周波数」とするのが自然です。このように電気工学の知識があれば、ωの単位を間違えることはなかったと考えています。