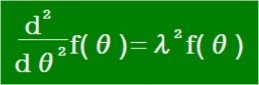【前回の記事を読む】学校で学ぶ数々の公式の「モヤモヤ感」筆者がそれ解き明かします!
第1章 文字積分法で拓く二階微分方程式の解法
第3節 過渡現象をあらわす二階微分方程式と解
【発展】これまでは次の簡単な二階微分方程式でした。
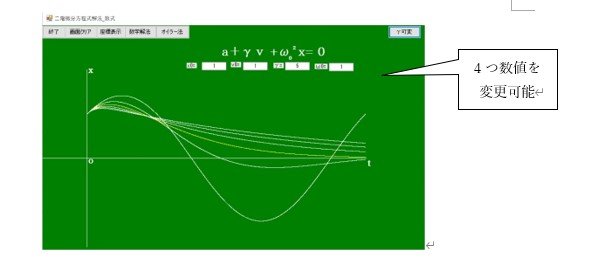
さらに、過渡現象を表わす次の二階微分方程式もあります。
変数はθではなくtです。時刻tの関数xは位置、vは速度、aは加速度です。この微分方程式の解は、数学の公式を使った解とオイラー法の解の2つがありますが、グラフは同一の形になることが確認できています。
【数学の公式を使った解】
数学で解は3通りになります。前出の関数θ=φtとしcosh(φt), sinh(φt), cos(φt), sin(φt)です。
過渡現象を表わすグラフです。γとω0の大小関係で、数式が異なります。
ソフトウェアのコードは長くなりますが、次のとおりです。
拙著『抽象化物理学の勧め』(2013年 PHPパブリッシング社刊行)から抜粋
Private Sub 計算主部()
Dim γ As Double
Dim ω0 As Double
Dim π As Double = Math.PI
Dim x, v, t, dt As Double
Dim x0, v0 As Double
Dim 区分 As Double
'ここから計算
dt = 0.001
x0 = Val(TextBox1.Text)
v0 = Val(TextBox2.Text)
γ = Val(TextBox3.Text)
ω0 = Val(TextBox4.Text)
区分 = Math.Abs(γ - 2.0 * ω0)
x = x0
v = v0
t = 0.0
Do
点(t, x, 青)
If (区分 < 0.001) Then
x = 関数2(x0, v0, t, γ)
Else
If (γ > 2.0 * ω0) Then
'関数1()
x = 関数1(x0, v0, t, γ, ω0)
Else
'関数3()
x = 関数3(x0, v0, t, γ, ω0)
End If
End If
t += dt
Loop Until t > 2.0 * π
'ここまで計算
End Sub
Private Function 関数1(ByVal x0 As Long, ByVal v0 As Double, ByVal t As Double, ByVal γ As Double, ByVal ω0 As Double) As Double
Dim φ, x As Double
φ = Math.Sqrt(γ * γ / 4 - ω0 * ω0)
x = Math.Exp(-γ * t / 2) * ((x0 * Math.Cosh(φ * t) + (v0 + γ * x0 / 2) * Math.Sinh(φ * t) / φ))
Return x
End Function
Private Function 関数2(ByVal x0 As Double, ByVal v0 As Double, ByVal t As Double, ByVal γ As Double) As Double
Dim x As Double
'φ=0.0 の時
x = Math.Exp(-γ * t / 2) * (x0 + v0 * t + γ * x0 * t / 2)
Return x
End Function
Private Function 関数3(ByVal x0 As Double, ByVal v0 As Double, ByVal t As Double, ByVal γ As Double, ByVal ω0 As Double) As Double
Dim φ, x As Double
φ = Math.Sqrt(ω0 * ω0 - γ * γ / 4)
x = Math.Exp(-γ * t / 2) * ((x0 * Math.Cos(φ * t) + (v0 + γ * x0 / 2) * Math.Sin(φ * t) / φ))
Return x
End Function
【オイラー法を使った解】
Private Sub 数値可変オイラー法()
Dim γ As Double
Dim ω0 As Double
Dim π As Double = Math.PI
Dim x, v, a, t As Double
Dim dt As Double
x = Val(TextBox1.Text)
v = Val(TextBox2.Text)
γ = Val(TextBox3.Text)
ω0 = Val(TextBox4.Text)
dt = 0.001
t = 0.0
Do
点(t, x, 白)
a = -γ * v - ω0 * ω0 * x
t += dt
x += v * dt
v += a * dt
Loop Until t > 2 * π
End Sub
【解を表わすディスプレイ画面】