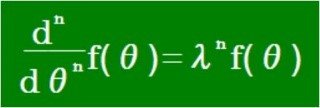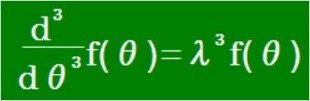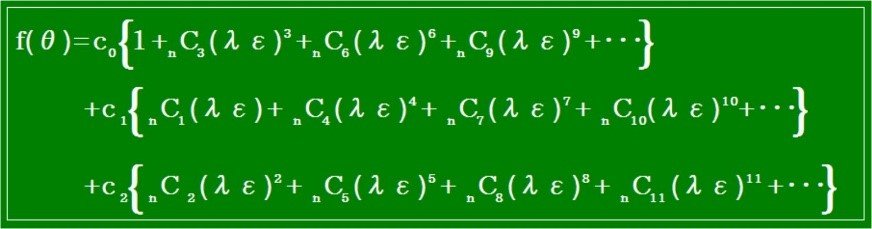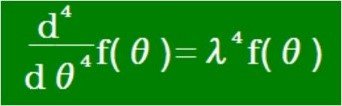第4節 高次微分方程式
【経過】二階微分方程式の解法を発表したのは2000年で、拙著『微積分学の大革命』に記載しました。
それまでは、解がcosθとsinθになることを知った上での解法ばかりでした。つまり、納得できる二階微分方程式の解法がなかったのです。解の形が具体的に冪関数として現れたのは『未定係数法』でした。
1970年当時は未定係数法は理論が不明でも解を得られる解法とされていましたが、物理学や化学で結構使われていました。
二階微分方程式の解法と同様な解法で三階微分方程式を解いた例を見たことがありません。つまり、数学には論理的な解法はなっかったのです。このモヤモヤ感は30年以上も続きました。
三階微分方程式の解を『微積分学の大革命』に記載しました。
【発展】同様な推論で、次のn階微分方程式の解を推測できます。
まず、n=3の三階微分方程式に関しては次のようになります。
三階微分方程式の解
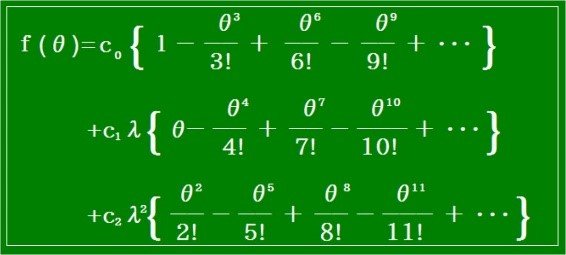
第1章の第1節 二階微分方程式の解法の「変換公式」を使い次式になります。
λ=cos(π/3)+isin(π/3)=ei(π/3)とし、λ3= eiπ=-1として次式になります。
【発展】四階微分方程式の基本解
最近の本の中に、電子の運動は四階微分方程式で表わせるという記述がありました。大学生の時に電気工学の実験で、それまでの数式には従わないという話を聞いたことがあります。四階微分方程式に従うかどうかを確認したい思いです。
【観察】この解をグラフにすると、曲線は進行するに従って振幅が拡大するsinθのようです。カーブが大きくなるのです。まるで落雷する場所を見つけているように思えるのはそのためかもしれません。
解は64ビットのコンピューターで、「オイラー法」を使って図示できます。