第2章 障害のある子どもの理解
順序数と集合数
また、抽象性という点では、大きな象を数えても「1、2」という数字になります。小さな蟻を数えてもやはり、同じ「1、2」の数字に置き換えることができます。さらに、この数の概念は猫を「1、2、3」と数えても、「3番目の猫」と「3匹の猫」という概念の二面性をもっています。
数には、物事を考えるときの汎用性があります。数には順序数、集合数という2つの概念の側面があります（図1）。
[図1] 数概念の二面性
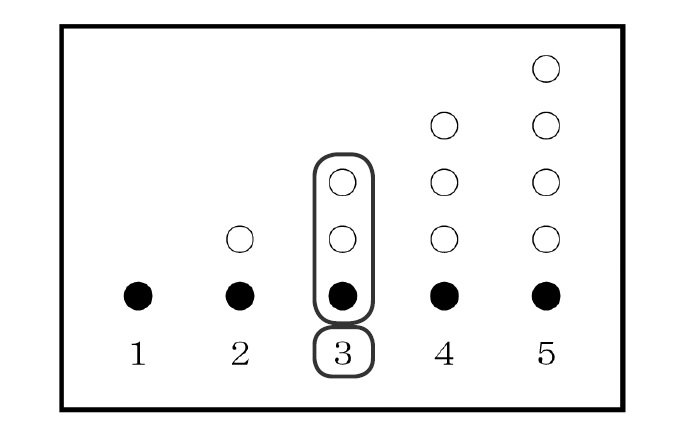
図1の黒丸は順序数としての数です。白丸は、まとまりとしての集合数です。数を量として覚えていくためには、集合数としての数概念を覚えていく必要があります。
図2は数概念を図式化したものです。数概念は、「具体物」と「数詞」と「数字」の3つの関係が結びつく必要があります。
[図2] 数概念の関係
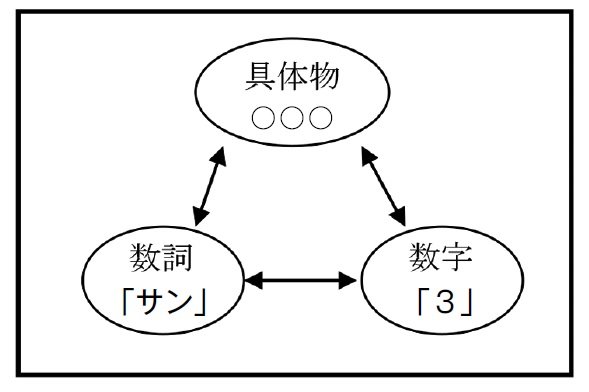
たとえば、「○○○」（具体物）な○を見て、「サン」（数詞）と「3」（数字）が、相互に結びつかないと、たし算、ひき算はできるようになりません。たし算をするためには、「両方を合わせる」や「だんだんに増える」といった操作概念がわかる必要があります。
ひき算をするためには「あるものをひいたら残りはいくつ」「こっちとあっちのどちらが多いか、少ないかの差」を求めるという操作概念を身につけていくことが必要です。子どもが自動車を見て、そらんじるように数えて「サン」と言っても、はたして「3台」として認識しているのか、ただなんとなく言葉のうえで「サン」と言っているのかわかりません。
