【人気記事】「非行」に走った青年時代…医者になった私が当時を思い出すと『腐ったみかんが医者になった日』
第4章 三角関数の公式
第3節 二倍角の公式
microsoft社の入社試験の問題がヒントになりました。二倍角の公式です。[rad]を省略しています。
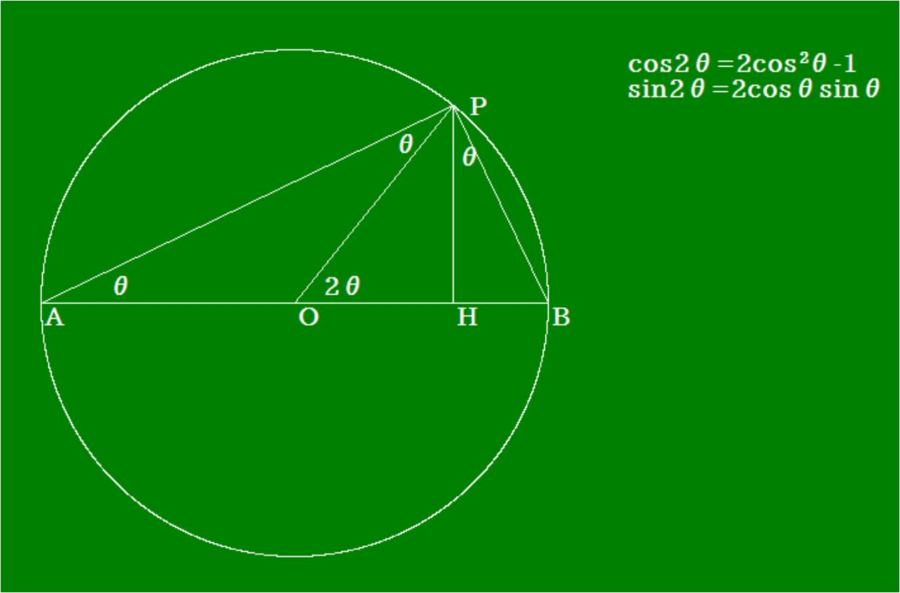
半径1の円で∠PAB=θ[rad]の時に、次の値をもとめよ。ただし、長さは無名数とする。
問1 弧PBの長さ 答 2θ
問2 弦PBの長さ 答 2sinθ
問3 弦APの長さ 答 2cosθ
問4 垂線PHの長さ 答 sin2θまたは2cosθsinθ
問5 線分OHの長さ 答 cos2θまたは2cos2θ-1
【感想】この問題で難問と思われるのは、弧PB=2θです。
OB=OA=1 と∠BOP=2θ[rad] から 弧度法の新定義によって弧PB =2θです。
第4節 扇形の面積公式
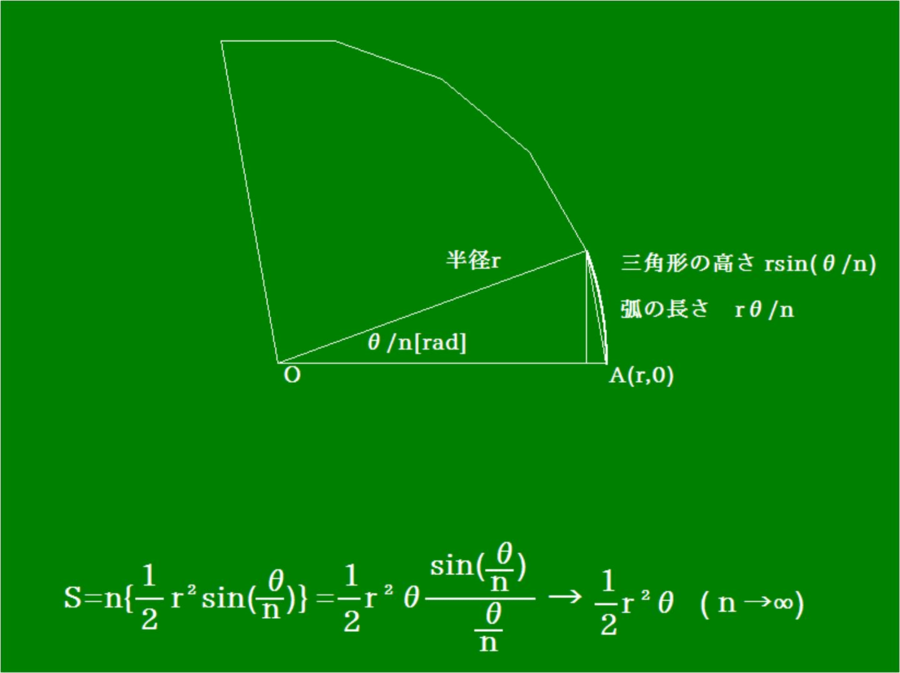
・半径rで中心角がθの扇形をn等分した図です。作図の都合でn=5とします。
n等分してできる三角形の面積をn倍すると、もとの扇形の面積になります。
式を変形してn→∞ とするとS=r2θ/2 となります。θ=2πで円の時はπr2となります。
・θ→0の時sinθ→θとなる証明ができていますから扇形の面積は証明できました。
【注目】2022年までの数学では、扇形の面積をもとめるときには次の比例式を使いました。
θ:2π=S:πr2
円の面積がπr2になる証明をしなければ不完全な解説になりますが、全く無視されています。