第3章 論理図解を使う弧度法の新定義
第5節 円弧の長さ
【案内】弧度法の定義に座標は使われていません。しかし、座標系で点の座標を加えないと定義が不十分になることに気づきます。次は論理を図解した弧度法の定義です。
・単位円における弧
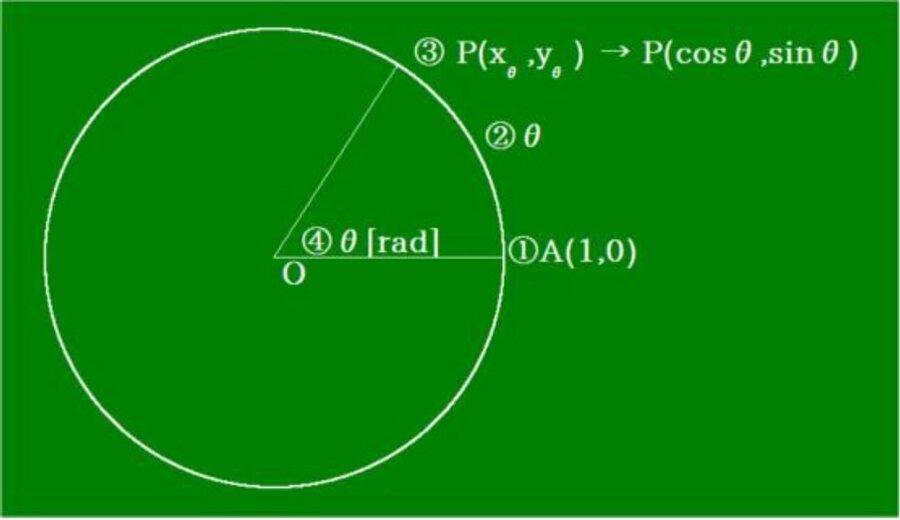
・弧度法の新定義
・「θで点P(xθ,yθ)の座標は特定できるのに、記載されている本が全くなかった」のです。高校生の時以来の弧度法のモヤモヤ感は三角関数を考慮していない解説のためでした。
・「第3章第3節 弧と中心角との関係」から、弧OP=θとするとP(cosθ,sinθ)となることが証明されています。従って、解説図ではP(xθ,yθ)→P(cosθ,sinθ) と明示しました。
・弧度法が理解されにくい理由は論理が逆になっているからです。単位円で、中心角をθ[rad]としたときに弧の長さをθ[rad]とするわけにはいきません。θが正しいからです。正しい論理は、弧の長さθが確定すれば、角度としてθ[rad]を定義できるのです。
単位円の弧の長さθ → 中心角θ[rad]
・弧度法を使った三角関数には多くの解説がありますが、「簡単に記憶できる三角関数の公式」とか「簡単に理解できる三角関数」という類の解説ばかりで「本当は難しい三角関数」という解説がありません。
はなはだしい嘘をつかれているようで、モヤモヤ感や不信感も生まれます。
・弧度法を正確に解説せず、π[rad]=180[°]の変換へミスリードした教科書への不信感があります。
・「弧度法と連立微分方程式と二階微分方程式の3領域にまたがる本当は難しい三角関数」という解説変更が必要な時にきていると考えます。さらに、考察に必要な道具として「文字積分法と論理図解」を挙げたいのです。
【感想】微積分や三角関数などの理系のモヤモヤする箇所を他の方に伝えても、「どこがモヤモヤしているというの?」と返答されるのを非常に恐れました。さらに「モヤモヤ感はありませんか?」と問えば「モヤモヤしているのはあなたでしょう」と対人攻撃に変化することを警戒しました。その結果、微積分や三角関数の疑問点を時間をかけて自分で解決しようと決心しました。
具体的な目標は「単振動」を表わす二階微分方程式 a=-ω2 のいままでの数学にはない解法でした。浜田哲夫教授からコンピューターによる数値積分の授業がありましたので、「オイラー法」という最も原始的な解法で計算しようと考えました。
2000年のコンピューターの能力では微小な時間間隔を設定できませんでしたが、2013年になって64ビットのコンピューターを使い、オイラー法で単振動を追跡できました。
さらに、過渡現象を表わす二階微分方程式 a+γv+ω02x=0を使い、数学による厳密解で描いた曲線とオイラー法で描いた曲線が一致することをディスプレイ上で示すことができました。『抽象化物理学の勧め』に記載。