第4章 三角関数の公式
三角関数が理解されると、複素数まで範囲を広げて今までの知識を整理する必要を感じます。
この章では、
・平面座標における加法定理
・複素平面における加法定理
・二倍角の公式
・扇形の面積の公式
を解説します。
第1節 平面座標における加法定理
加法定理を証明するときに、最も面倒なのは、正確に作図することです。個人で作図するのは面倒ですから、教科書や参考書の図に頼ることになります。コンピューターによる作図も、線を引く小プログラムを作成するのは難しいのです。しかし、複素数を使った加法定理の証明は簡単です。
加法定理を理解するには、作図で理解し複素数で数式を記憶するのが現実的です。
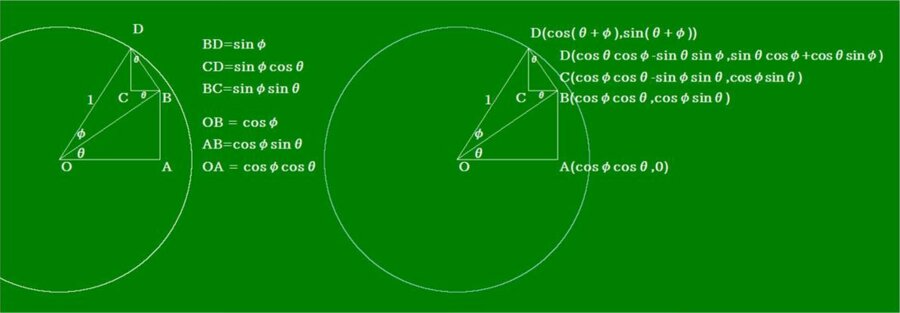
・加法定理の論理図解
Dの座標は2通りあります。これが加法定理の公式となっています。
D(cos(θ+φ), cos(θ+φ))
D(cosθcosφ-sinθsinsφ,sinθcosφ+cosθsinφ))
第2節 複素平面における加法定理
【案内】複素数表示は記憶の助けとなります。
・複素平面での加法定理の表現
平面座標の点(cosθ,sinθ)は複素平面ではcosθ+isinθと表現されます。
加法定理からもわかっていることがあります。
cos(θ+φ)=cosθcosφ-sinθsinφ sin(θ+φ)= cosθsinφ+sinθcosφ
次の計算ができます。
・ cos(θ+φ) + isin(θ+φ)= (cosθcosφ-sinθsinφ)+i(cosθsinφ+sinθcosφ)
・(cosθ+isinθ)(cosφ+isinφ) = (cosθcosφ-sinθsinφ)+i(cosθsinφ+sinθcosφ)
この2式から
cos(θ+φ) + isin(θ+φ)= (cosθ+isinθ)(cosφ+isinφ)
さらに

を使って書き換えると、加法定理は次式になります。
ei(θ+φ) = eiθeiφ
次の定理へと進みます。
ei・nθ = ( eiθ)n ド・モアブルの定理
図を描いて加法定理を証明するのは手間がかかりますが、複素数で記憶するのは簡単です。