第3章 論理図解を使う弧度法の新定義
第3節 弧と中心角との関係
数学の単位円において、弧の長さθには単位はなく、中心角には単位[rad]が付きθ[rad]になります。
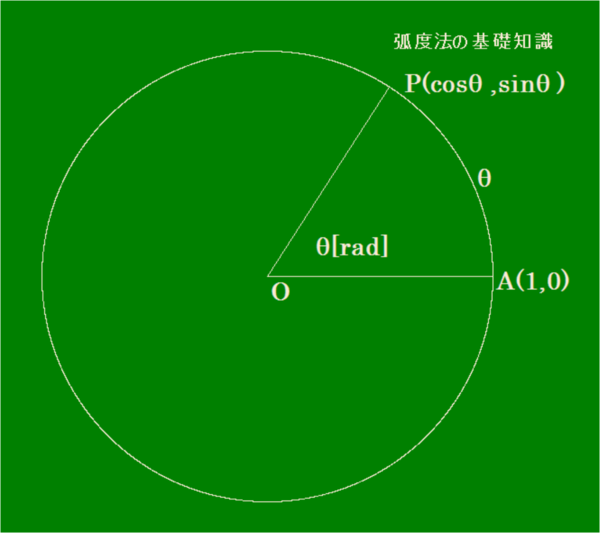
■弧度法の基礎知識
θとθ[rad]と点P(cosθsinθ)のように3つを同時に表示します。「第1節 等速円運動の動点の射影は単振動をする」において「A(1,0)とP(cosθ,sinθ)とするときに、弧AP=θとなる証明」をこの節で証明します。三角関数が明確になります。
・cosθとsinθを次のように定義したときに、それらの微分を調べます。


・記号の limの代わりにεを使って微分の結果を表わします。
・円周上の点P(cosθ,sinθ)と近くのQ(cos(θ+ε),sin(θ+ε))で、εの意味を調べます。
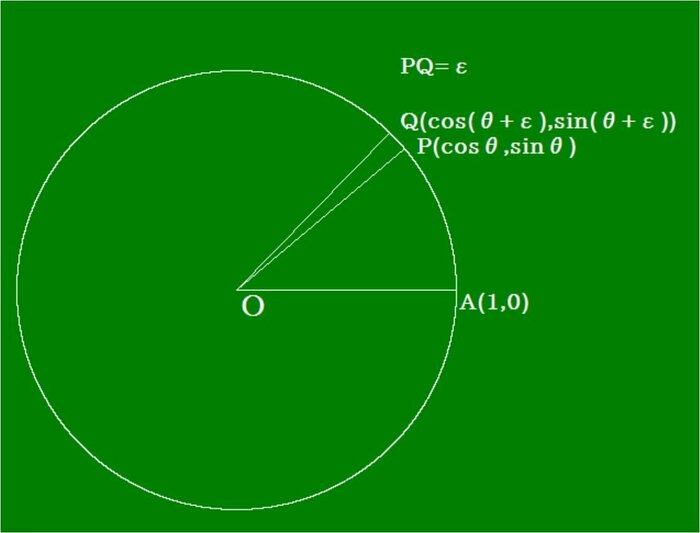

【結論】 cos(θ+ε)とsin(θ+ε)の中で、「θの増分εは弧の長さの増分ε」に対応します。
弧の長さがnεならば、(cos(nε),sin(nε))となり、nε=θと置き換えて、A(1,0)からの弧の長さがθならばP(cosθ,sinθ)になります。
【注目】弧と中心角の関係は次のようになります。
弧PQ=εで ∠POQ =ε[rad] であり、
AP=θで ∠AOP =θ[rad] となります。
【別解】複素数を使うと簡略化されます。Pの複素数をZ、Qの複素数をZ+dZとすると、
dZ=ei(θ+ε)-eiθ=eiθ(eiε-1)=eiθ{(cosε+isinε)-1}
ε→ならば dZ→ eiθ(1+iε-1) さらに dZ→eiθ(iε)
∴ iεは、Z点で反時計周りにπ/2回転し、長さはεとなることを意味します。