第1クラスターの相関分析
図表1から第2クラスターの特徴が『ランキング調査』にも『希望調査』にも参加せず、導入講義の成績状況が芳しくない学生が属していることが分かった。そこで、ここでは第1クラスターの特徴をKendallの順位相関係数から確認しよう。その結果が図表2に示されている。

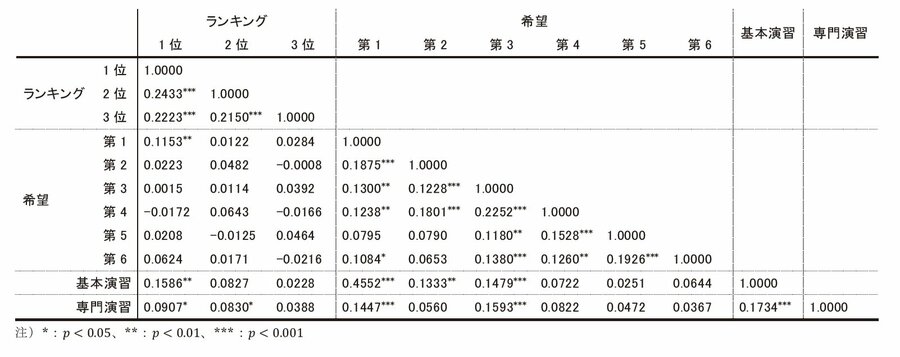
まず、『ランキング調査』の回答と他の変数間の相関係数から確認する。これを見ると、『ランキング調査』内の諸変数、すなわち1~3位間相互に弱い正の相関が見られた。
次に、『ランキング調査』と『希望調査』の諸変数間の相関を見ると、ランキング1位と第1希望の係数のみが有意だった。この結果は該当する相関係数が有意にゼロでないと言えるが、係数の値が0.1153と相関の目安である0.2未満なため、ほぼ相関がないか、あったとしてもごく弱いと判断できる。
『ランキング調査』で選んだコースと『希望調査』で選んだコースが必ずしも一致していないという予想が、ここで確認された格好である。
最後に、『ランキング調査』と基本および専門演習との相関を確認する。これを見ると、ランキング1位と基本・専門それぞれの演習と、2位と専門演習との間にそれぞれ有意な正の相関を示す係数があったが、先述の理由からほぼ無相関と判断していいだろう。
以上の結果は、導入講義をきっかけにして基本・専門演習へとたどるコース選択の接続が、本学部の狙い通りではないことを示唆している。次に、『希望調査』の回答と基本および専門演習との相関を見てみよう。
その前に、『希望調査』内の諸変数間の相関を確認すると、第1希望と第5希望、第2希望と第5・6希望との相関は有意でなく他は有意という結果だった。しかし、弱いながらも正の相関があると判断できるのは第3希望と第4希望の相関のみであって、この結果は学生がコースに対して強いこだわりを持っている訳ではないことを示している。
一方、『希望調査』と基本演習との相関を確認すると、第1希望との間に中程度の正の相関があった。先述の通り、基本演習への学生の割り振りは第1希望から行われるから、この結果自体はごく自然であろう。第2・3希望との間にも正の相関が確認できたが、ほぼ相関していないと見ていいだろう。最後に、『希望調査』と専門演習間の相関を確認すると、第1・3希望と正の相関があったがこれもほぼ無相関だと言える。















