第二章 破 絶歌
なぜ人を殺してはいけないのか?
ここで少し数学論理による命題という視点から考えてみたいと思います。なお、程度は高校一年の数学Aの範囲です。命題とはある判断を言葉や記号で表現したものであり、それが正しいか正しくないか誰が考えても明確に決められるものを言います。
つまり真偽の判定が下せないような曖昧なものは命題ではありません。命題が正しいことを「真」と言い、正しくないことを「偽」と言います。即ち「戦争→悪」のようなものは、実は命題ではありません。あるいは「偽なる命題」です。「戦争」や「悪」を完全には定義できないからです。
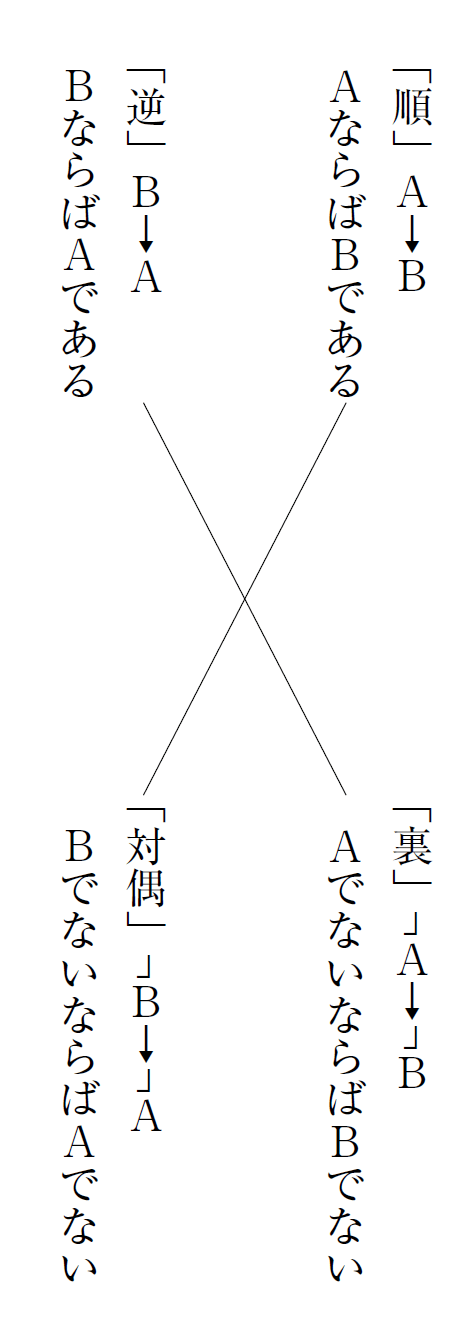
その命題「AならばBである」は「A」も「B」も共に真偽の判定ができることが条件です。その時、Aはこの命題の仮定でありBであるための十分条件と言い、Bはこの命題の結論でありAであるための必要条件と言います。その命題「AならばBである」を「A→B」と書き、これを「順」と呼ぶ時、「B→A」を「逆」と呼びます。また「Aの否定文」、つまり「Aでない」を「┘A」と書き、「AでないならばBでない」を「┘A→┘B」と書き、これを「裏」と呼びます。
その逆「┘B→┘A」を「対偶」と呼びます。この時「A→B」が真であれば、その対偶「┘B→┘A」は常に真ですが、その逆「B→A」、及び裏「┘A→┘B」は常に真とは限らない、という法則があるのです。
さて「自分は殺されたくないので、他人を殺してはならない」という否定的黄金律をもって回答した人々は、実は全員が神を知らないか、神を否定する側にいる人でした。自分の理屈だけが頼りの酒鬼薔薇聖斗や佐川一政に対し、論理の正しさと論拠、その真偽の証明によって彼らの信念を撤回させたいのであれば、まずは自らの論理を点検し「実験」してみなければなりません。
数学文に書きかえた時の「A→B」が真であれば、その対偶「┘B→┘A」も常に真であるという法則があるからです。つまりは対偶を調べればいいだけの話です。「自分は殺されたくない→他人を殺してはならない」の対偶は、「他人を殺してよい→自分は殺されたい」です。
これでは回答者全員が自殺願望者と殺人鬼です。つまり元々の命題が偽であり、説得力などなく、命題ですらありません。
命題として扱うためには、Aに含まれる全ての人間が「自分は殺されたくない」と明示しなければなりません。同時にBに含まれる全ての人間も「他人を殺してはならない」と自覚していることです。
であれば数学文の命題としては、成立可能です。しかし逆にそのような人間しかこの世に存在しないのであれば、つまり全ての人間が堕落前のアダムとエバのようであるならば、そもそも証明自体が不要であり無意味です。人間は当たり前のことを当たり前だと言うことはできても、それを証明という手法に乗せるのは不可能なのかもしれません。それが理性の限界であり、数学の限界なのかもしれません。
会津藩校「什の掟」の結語に記された如く、新島八重さんに倣い「ならぬことはならぬものです」と堂々と言わねばなりません。