5）定常状態での最高血中濃度の推定

1）−（2）では定常状態の話をしましたが、添付文書の数値から定常状態の最高血中濃度を知ることはできないでしょうかという問題です。定常状態ではある一定の血中濃度間を上下動しますが、そのときの最高血中濃度を定常状態での最高血中濃度Cssmaxとします。そして定常状態での最低血中濃度をCssminとします。さらに単回投与時の最高血中濃度をCmaxとします。結論から言うと、定常状態の最高血中濃度は（式1）で表現されます。

（式1）

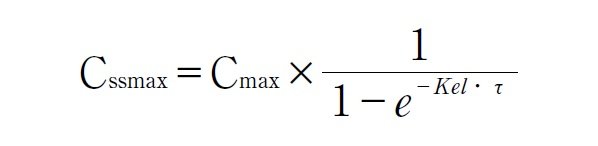
ここでKelは消失速度定数（1/h）、τは投与間隔（h）になります。上記の右辺の分数部分は蓄積率と呼ばれています。この式は薬が血中から1次速度式で減少するとした場合に成り立つ式ですから、別次元速度で消失する薬では誤差が出てきますが、ほとんどの薬で成立するのでほぼ安心して利用できます。

詳細は省きますが、1次速度で減少する場合は消失速度定数Kelと半減期t1/2の間には次の関係があります。Kel＝0.693/t1/2そこで式1のKelをt1/2で置き換えた時の蓄積率は表1で示せます。

1）−（2）で紹介したアムロジピンは投与間隔τが24時間、半減期t1/2が36時間でしたから、τ/t1/2≒0.7なので蓄積率は表1から2.6と分かります。定常状態のCmaxが初回投与Cmaxの大体2.6倍になっているのが、先のアムロジピンの血中濃度推移のグラフからも分かるかと思います。

写真を拡大 ［表1］蓄積率 出典元：菅野彊著『わかる臨床薬物動態理論の応用』医薬ジャーナル社（2001年）

まとめ

実際の薬局業務の中で患者さんの血中濃度を知る機会はほとんどないですし、保険診療対象となる血中濃度測定の薬は限定されているため大抵の患者さんの薬の血中濃度は測定されていません。従って、この表1は定常状態になったときは単回投与のときの何倍くらいの血中濃度に上昇しているかの推定や、後で出てくる腎機能障害のときにはどれくらいまで血中濃度が上昇するかの目安になると思われますので、現場で推定する手法として有用だと思います。